Как составить каноническое уравнение. Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

• прямые пересекаются;

• прямые параллельны;

• прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение . Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

. C = 0, А ≠0, В ≠ 0 - прямая проходит через начало координат

. А = 0, В ≠0, С ≠0 { By + C = 0} - прямая параллельна оси Ох

. В = 0, А ≠0, С ≠ 0 { Ax + C = 0} - прямая параллельна оси Оу

. В = С = 0, А ≠0 - прямая совпадает с осью Оу

. А = С = 0, В ≠0 - прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких - либо заданных

начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение . В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой, заданной уравнением

Ах + Ву + С = 0.

Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение . Составим при А = 3 и В = -1 уравнение прямой: 3х - у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 - 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х - у - 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой ,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х 2 и х = х 1 , если х 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой .

Пример . Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение . Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение . Каждый ненулевой вектор (α 1 , α 2) , компоненты которого удовлетворяют условию

Аα 1 + Вα 2 = 0 называется направляющим вектором прямой.

Ах + Ву + С = 0.

Пример . Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение . Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3 , т.е. искомое уравнение:

х + у - 3 = 0

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на -С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b - координатой точки пересечения прямой с осью Оу.

Пример . Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 - нормальное уравнение прямой .

Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0.

р - длина перпендикуляра, опущенного из начала координат на прямую,

а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример . Дано общее уравнение прямой 12х - 5у - 65 = 0 . Требуется написать различные типы уравнений

этой прямой.

Уравнение этой прямой в отрезках :

Уравнение этой прямой с угловым коэффициентом : (делим на 5)

Уравнение прямой :

cos φ = 12/13; sin φ= -5/13; p = 5.

Следует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые,

параллельные осям или проходящие через начало координат.

Угол между прямыми на плоскости.

Определение . Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми

будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны,

если k 1 = -1/ k 2 .

Теорема .

Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты

А 1 = λА, В 1 = λВ . Если еще и С 1 = λС , то прямые совпадают. Координаты точки пересечения двух прямых

находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.

Определение . Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b

представляется уравнением:

Расстояние от точки до прямой.

Теорема . Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С = 0 определяется как:

Доказательство . Пусть точка М 1 (х 1 , у 1) - основание перпендикуляра, опущенного из точки М на заданную

прямую. Тогда расстояние между точками М и М 1 :

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы - это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно

заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Пусть l - некоторая прямая пространства. Как и в планиметрии, любой вектор

а =/= 0, коллинеарный прямой l , называется направляющим вектором этой прямой.

Положение прямой в пространстве полностью определяется заданием направляющего вектора и точки, принадлежащей прямой.

Пусть прямая l с направляющим вектором а проходит через точку M 0 , а М - произвольная точка пространства. Очевидно, что точка М (рис. 197) принадлежит прямой l тогда и только тогда, когда вектор \(\overrightarrow{M_0 M}\) коллинеарен вектору а , т. е.

\(\overrightarrow{M_0 M}\) = ta , t \(\in \) R . (1)

Если точки М и M 0 заданы своими радиус-векторами r и r 0 (рис. 198) относительно некоторой точки О пространства, то \(\overrightarrow{M_0 M}\) = r - r 0 , и уравнение (1) принимает вид

r = r 0 + ta , t \(\in \) R . (2)

Уравнения (1) и (2) называются векторно-параметрическими уравнениями прямой. Переменная t в векторно-параметрических уравнениях прямой называется параметром .

Пусть точка M 0 прямой l и направляющий вектор а заданы своими координатами:

M 0 (х 0 ; у 0 , z 0), а = (а 1 ; а 2 ; а 3).

Тогда, если (х; у; z ) - координаты произвольной точки М прямой l , то

\(\overrightarrow{M_0 M} \) = (х - х 0 ; у - у 0 ; z - z 0)

и векторное уравнение (1) равносильно следующим трем уравнениям:

х - х 0 = tа 1 , у - у 0 = tа 2 , z - z 0 = tа 3

$$ \begin{cases} x = x_0 + ta_1 \\ y = y_0 + ta_2 \\ z = z_0 + ta_3, \;\;t\in R\end{cases} (3)$$

Уравнения (3) называются параметрическими уравнениями прямой в пространстве.

Задача 1. Написать параметрические уравнения прямой, проходящей через точку

M 0 (-3; 2; 4) и имеющей направляющий вектор а = (2; -5; 3).

В данном случае х 0 = -3, у 0 = 2, z 0 = 4; а 1 = 2; а 2 = -5; а 3 = 3. Подставив эти значения в формулы (3), получим параметрические уравнения данной прямой

$$ \begin{cases} x = -3 - 2t \\ y = 2 - 5t \\ z = 4 + 3t, \;\;t\in R\end{cases} $$

Исключим параметр t из уравнений (3). Это можно сделать, так как а =/= 0, и поэтому одна из координат вектора а заведомо отлична от нуля.

Пусть сначала все координаты отличны от нуля. Тогда

$$ t=\frac{x-x_0}{a_1},\;\;t=\frac{y-y_0}{a_2},\;\;t=\frac{z-z_0}{a_3} $$

и, следовательно,

$$ \frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}=\frac{z-z_0}{a_3} \;\; (4)$$

Эти уравнения называются каноническими уравнениями прямой .

Заметим, что уравнения (4) образуют систему двух уравнений с тремя переменными х, у и z.

Если в уравнениях (3) одна из координат вектора а , например а 1 равна нулю, то, исключив параметр t , снова получим систему двух уравнений с тремя переменными х, у и z :

\(x=x_0, \;\; \frac{y-y_0}{a_2}=\frac{z-z_0}{a_3}\)

Эти уравнения также называются каноническими уравнениями прямой. Для единообразия их также условно записывают в виде (4)

\(\frac{x-x_0}{0}=\frac{y-y_0}{a_2}=\frac{z-z_0}{a_3}\)

считая, что если знаменатель равен нулю, то равен нулю и соответствующий числитель. Эти уравнения являются уравнениями прямой, проходящей через точку M 0 (х 0 ; у 0 , z 0) параллельно координатной плоскости yOz , так как этой плоскости параллелен ее направляющий вектор (0; а 2 ; а 3).

Наконец, если в уравнениях (3) две координаты вектора а , например а 1 и а 2 равны нулю, то эти уравнения принимают вид

х = х 0 , y = у 0 , z = z 0 + ta 3 , t \(\in \) R .

Это уравнения прямой, проходящей через точку M 0 (х 0 ; у 0 ; z 0) параллельно оси Oz . Для такой прямой х = х 0 , y = у 0 , a z - любое число. И в этом случае для единообразия уравнения прямой можно записывать (с той же оговоркой) в виде (4)

\(\frac{x-x_0}{0}=\frac{y-y_0}{0}=\frac{z-z_0}{a_3}\)

Таким образом, для любой прямой пространства можно написать канонические уравнения (4), и, наоборот, любое уравнение вида (4) при условии, что хотя бы один из коэффициентов а 1 , а 2 , а 3 не равен нулю, задает некоторую прямую пространства.

Задача 2. Написать канонические уравнения прямой, проходящей через точку M 0 (- 1; 1, 7) параллельно вектору а = (1; 2; 3).

Уравнения (4) в данном случае записываются слeдующим образом:

\(\frac{x+1}{1}=\frac{y-1}{2}=\frac{z-7}{3}\)

Выведем уравнения прямой, проходящей через две данные точки M 1 (х 1 ; у 1 ; z 1) и

M 2 (х 2 ; у 2 ; z 2). Очевидно, что за направляющий вектор этой прямой можно взять вектор a = (х 2 - х 1 ; у 2 - у 1 ; z 2 - z 1), а за точку М 0 , через которую проходит прямая, например, точку M 1 . Тогда уравнения (4) запишутся так:

\(\frac{x-x_1}{x_2 - x_1}=\frac{y-y_1}{y_2 - y_1}=\frac{z-z_1}{z_2 - z_1}\) (5)

Это и есть уравнения прямой, проходящей через две точки M 1 (х 1 ; у 1 ; z 1) и

M 2 (х 2 ; у 2 ; z 2).

Задача 3. Написать уравнения прямой, проходящей через точки M 1 (-4; 1; -3) и M 2 (-5; 0; 3).

В данном случае х 1 = -4, у 1 = 1, z 1 = -3, х 2 = -5, у 2 = 0, z 2 = 3. Подставив эти значения в формулы (5), получим

\(\frac{x+4}{-1}=\frac{y-1}{-1}=\frac{z+3}{6}\)

Задача 4. Написать уравнения прямой, проходящей через точки M 1 (3; -2; 1) и

M 2 (5; -2; 1 / 2).

После подстановки координат точек M 1 и M 2 в уравнения (5) получим

\(\frac{x-3}{2}=\frac{y+2}{0}=\frac{z-1}{-\frac{1}{2}}\)

3.1. Канонические уравнения прямой.

Пусть в системе координат Oxyz дана прямая, которая проходит через точку

(см. рис.18).Обозначим через
вектор, параллельный данной прямой. Векторназываетсянаправляющим вектором прямой. Возьмем на прямой точку
и рассмотрим вектор Векторы
коллинеарны, следовательно, их соответствующие координаты пропорциональны:

(3.3.1 )

Эти уравнения называются каноническими уравнениями прямой.

Пример: Написать уравнения прямой, проходящей через точку M(1, 2, –1) параллельно вектору

Решение: Вектор является направляющим вектором искомой прямой. Применяя формулы (3.1.1), получим:

Это канонические уравнения прямой.

Замечание: Обращение в нуль одного из знаменателей означает обращение в нуль соответствующего числителя, то есть y – 2 = 0; y = 2. Данная прямая лежит в плоскости y = 2, параллельной плоскости Oxz.

3.2. Параметрические уравнения прямой.

Пусть прямая задана каноническими уравнениями

Обозначим
тогда
Величина t называется параметром и может принимать любые значения:
.

Выразим x, y и z через t:

(3.2.1 )

Полученные уравнения называются параметрическими уравнениями прямой.

Пример 1: Составить параметрические уравнения прямой, проходящей через точку M (1, 2, –1) параллельно вектору

Решение: Канонические уравнения этой прямой получены в примере пункта 3.1:

Для нахождения параметрических уравнений прямой применим вывод формул (3.2.1):

Итак,
- параметрические уравнения данной прямой.

Ответ :

Пример 2. Составить параметрические уравнения прямой, проходящей через точку M (–1, 0, 1) параллельно вектору
гдеA (2, 1, –1), B (–1, 3, 2).

Решение: Вектор
является направляющим вектором искомой прямой.

Найдем вектор
.

= (–3; 2; 3). По формулам (3.2.1) запишем уравнения прямой:

- это искомые параметрические уравнения прямой.

3.3. Уравнения прямой, проходящей через две заданные точки.

Через две заданные точки в пространстве проходит единственная прямая (см. рис.20). Пусть даны точки Вектор
можно принять за направляющий вектор данной прямой. Тогда уравнения прямой находим по формулам (3.1.1):
).

(3.3.1)

Пример 1. Составить канонические и параметрические уравнения прямой, проходящей через точки

Решение : Применяем формулу (3.3.1)

Получили канонические уравнения прямой. Для получения параметрических уравнений применим вывод формул (3.2.1). Получим

- это параметрические уравнения прямой.

Пример 2. Составить канонические и параметрические уравнения прямой, проходящей через точки

Решение : По формулам (3.3.1) получим:

Это канонические уравнения.

Переходим к параметрическим уравнениям:

- параметрические уравнения.

Полученная прямая параллельна оси oz (см. рис.21).

Пусть в пространстве даны две плоскости

Если эти плоскости не совпадают и не параллельны, то они пересекаются по прямой:

Эта система двух линейных уравнений задает прямую как линию пересечения двух плоскостей. От уравнений (3.4.1) можно перейти к каноническим уравнениям (3.1.1) или параметрическим уравнениям (3.2.1). Для этого необходимо найти точку
лежащую на прямой, и направляющий векторКоординаты точки
получим из системы (3.4.1), придав одной из координат произвольное значение (например,z = 0). За направляющий вектор можно взять векторное произведение векторовто есть

Пример 1. Составить канонические уравнения прямой

Решение: Пусть z = 0. Решим систему

Сложив эти уравнения, получим: 3x + 6 = 0
x = –2. Подставим найденное значение x = –2 в первое уравнение системы и получим: –2 + y + 1 = 0
y = 1.

Итак, точка
лежит на искомой прямой.

Для нахождения направляющего вектора прямой запишем нормальные векторы плоскостей: и найдем их векторное произведение:

Уравнения прямой находим по формулам (3.1.1):

Ответ:
.

Другой способ: Канонические и параметрические уравнения прямой (3.4.1) легко получить, найдя две различные точки на прямой из системы (3.4.1), а затем применив формулы (3.3.1) и вывод формул (3.2.1).

Пример 2. Составить канонические и параметрические уравнения прямой

Решение: Пусть y = 0. Тогда система примет вид:

Сложив уравнения, получим: 2x + 4 = 0; x = –2. Подставим x = –2 во второе уравнение системы и получим: –2 –z +1 = 0
z = –1. Итак, нашли точку

Для нахождения второй точки положим x = 0. Будем иметь:

То есть

Получили канонические уравнения прямой.

Составим параметрические уравнения прямой:

Ответ :
;
.

3.5. Взаимное расположение двух прямых в пространстве.

Пусть прямые
заданы уравнениями:

:
;
:

.

Под углом между этими прямыми понимают угол между их направляющими векторами (см. рис.22). Этот уголнаходим по формуле из векторной алгебры:
или

(3.5.1)

Если прямые
перпендикулярны (
),то
Следовательно,

Это условие перпендикулярности двух прямых в пространстве.

Если прямые
параллельны (
),то их направляющие векторы коллинеарны (
), то есть

(3.5.3 )

Это условие параллельности двух прямых в пространстве.

Пример 1. Найти угол между прямыми:

а).
и

б).
и

Решение: а). Запишем направляющий вектор прямой
Найдем направляющий вектор
плоскостей, входящих в систему Затем найдем их векторное произведение:

(см. пример 1 пункта 3.4).

По формуле (3.5.1) получим:

Следовательно,

б). Запишем направляющие векторы данных прямых: Векторы
коллинеарны, так как их соответствующие координаты пропорциональны:

Значит прямые
параллельны (
), то есть

Ответ: а).
б).

Пример 2. Доказать перпендикулярность прямых:

и

Решение: Запишем направляющий вектор первой прямой

Найдем направляющий вектор второй прямой. Для этого находим нормальные векторы
плоскостей, входящих в систему: Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие перпендикулярности прямых (3.5.2):

Условие выполнено; следовательно, прямые перпендикулярны (
).

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

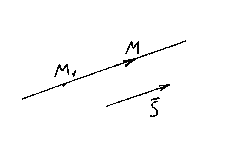
Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

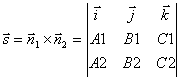Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Пусть в трехмерном пространстве зафиксирована Oxyz . Зададим в ней прямую. Выберем следующий способ задания прямой линии в пространстве : укажем точку, через которую проходит прямая a , и направляющий вектор прямой a . Будем считать, что точка лежит на прямой а и - направляющий вектор прямой а .

Очевидно, что множество точек трехмерного пространства определяет прямую а тогда и только тогда, когда векторы и коллинеарны.

Обратите внимание на следующие важные факты:

Приведем пару примеров канонических уравнений прямой в пространстве:

Составление канонических уравнений прямой в пространстве.

Итак, канонические уравнения прямой в фиксированной прямоугольной системе координат Oxyz в трехмерном пространстве вида соответствуют прямой линии, которая проходит через точку , а направляющим вектором этой прямой является вектор . Таким образом, если нам известен вид канонических уравнений прямой в пространстве, то мы можем сразу записать координаты направляющего вектора этой прямой, а если известны координаты направляющего вектора прямой и координаты некоторой точки этой прямой, то мы сразу можем записать ее канонические уравнения.

Покажем решения таких задач.

Пример.

Прямая в прямоугольной системе координат Oxyz в трехмерном пространстве задана каноническими уравнениями прямой вида . Напишите координаты всех направляющих векторов этой прямой.

Решение.

Числа, стоящие в знаменателях канонических уравнений прямой, являются соответствующими координатами направляющего вектора этой прямой, то есть, - один из направляющих векторов исходной прямой. Тогда множество всех направляющих векторов прямой можно задать как , где - параметр, принимающий любые действительные значения, кроме нуля.

Ответ:

Пример.

Напишите канонические уравнения прямой, которая в прямоугольной системе координат Oxyz в пространстве проходит через точку , а направляющий вектор прямой имеет координаты .

Решение.

Из условия имеем . То есть, у нас есть все данные, чтобы написать требуемые канонические уравнения прямой в пространстве. В нашем случае

.

Ответ:

Мы рассмотрели простейшую задачу на составление канонических уравнений прямой в заданной прямоугольной системе координат в трехмерном пространстве, когда известны координаты направляющего вектора прямой и координаты некоторой точки прямой. Однако намного чаще встречаются задачи, в которых сначала требуется найти координаты направляющего вектора прямой, а уже потом записывать канонические уравнения прямой. В качестве примера можно привести задачи на нахождение уравнений прямой, проходящей через заданную точку пространства параллельно заданной прямой и задачи на нахождение уравнений прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости .

Частные случаи канонических уравнений прямой в пространстве.

Мы уже отмечали, что одно или два из чисел в канонических уравнениях прямой в пространстве вида могут быть равны нулю. Тогда запись считается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как , где .

Давайте рассмотрим подробнее все эти частные случаи канонических уравнений прямой в пространстве.

Пусть , или , или , тогда канонические уравнения прямых имеют вид

или

или

В этих случаях в прямоугольной системе координат Oxyz в пространстве прямые лежат в плоскостях , или соответственно, которые параллельны координатным плоскостям Oyz , Oxz или Oxy соответственно (или совпадают с этими координатными плоскостями при , или ). На рисунке представлены примеры таких прямых.

При , или , или канонические уравнения прямых запишутся как


или


или


соответственно.

В этих случаях прямые параллельны координатным осям Oz , Oy или Ox соответственно (или совпадают с этими осями при , или ). Действительно, направляющие векторы рассматриваемых прямых имеют координаты , или , или , очевидно, что они коллинеарны векторам , или , или соответственно, где - направляющие векторы координатных прямых. Посмотрите иллюстрации к этим частным случаям канонических уравнений прямой в пространстве.

Осталось для закрепления материала этого пункта рассмотреть решения примеров.

Пример.

Напишите канонические уравнения координатных прямых Ox , Oy и Oz .

Решение.

Направляющими векторами координатных прямых Ox , Oy и Oz являются координатные векторы и соответственно. Кроме этого, координатные прямые проходят через начало координат – через точку . Теперь мы можем записать канонические уравнения координатных прямых Ox , Oy и Oz , они имеют вид и соответственно.

Ответ:

Канонические уравнения координатной прямой Ox , - канонические уравнения оси ординат Oy , - канонические уравнения оси аппликат.

Пример.

Составьте канонические уравнения прямой, которая в прямоугольной системе координат Oxyz в пространстве проходит через точку и параллельна оси ординат Oy .

Решение.

Так как прямая, канонические уравнения которой нам требуется составить, параллельна координатной оси Oy , то ее направляющим вектором является вектор . Тогда канонические уравнения этой прямой в пространстве имеют вид .

Ответ:

Канонические уравнения прямой проходящей через две заданные точки пространства.

Поставим себе задачу: написать канонические уравнения прямой, проходящей в прямоугольной системе координат Oxyz в трехмерном пространстве через две несовпадающие точки и .

В качестве направляющего вектора заданной прямой можно принять вектор (если больше нравиться вектор , то можно взять его). По известным координатам точек М 1 и М 2 можно вычислить координаты вектора : . Теперь мы можем записать канонические уравнения прямой, так как знаем координаты точки прямой (в нашем случае даже координаты двух точек М 1 и М 2 ), и знаем координаты ее направляющего вектора. Таким образом, заданная прямая в прямоугольной системе координат Oxyz в трехмерном пространстве определяется каноническими уравнениями вида или . Это и есть искомые канонические уравнения прямой, проходящей через две заданные точки пространства .

Пример.

Напишите канонические уравнения прямой, проходящей через две точки трехмерного пространства и .

Решение.

Из условия имеем . Подставляем эти данные в канонические уравнения прямой, проходящей через две точки :

Если воспользоваться каноническими уравнениями прямой вида , то получаем
.

Ответ:

или

Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.

Для решения некоторых задач канонические уравнения прямой в пространстве могут оказаться менее удобны, чем параметрические уравнения прямой в пространстве вида . А иногда предпочтительнее определить прямую линию в прямоугольной системе координат Oxyz в пространстве через уравнения двух пересекающихся плоскостей как . Поэтому встает задача перехода от канонических уравнений прямой в пространстве к параметрическим уравнениям прямой или к уравнениям двух пересекающихся плоскостей.

От уравнений прямой в каноническом виде легко перейти к параметрическим уравнениям этой прямой. Для этого требуется каждую из дробей в канонических уравнениях прямой в пространстве принять равной параметру и разрешить полученные уравнения относительно переменных x , y и z :

При этом параметр может принимать любые действительные значения (так как переменные x , y и z могут принимать какие угодно действительные значения).

Теперь покажем, как из канонических уравнений прямой получить уравнения двух пересекающихся плоскостей, определяющих эту же прямую.

Двойное равенство по сути представляет собой систему из трех уравнений вида (мы попарно приравняли дроби из канонических уравнений прямой). Так как пропорцию мы понимаем как , то

Итак, мы получили
.

Так как числа a x , a y и a z одновременно не равны нулю, то основной матрицы полученной системы равен двум, так как

а хотя бы один из определителей второго порядка


отличен от нуля.

Следовательно, из системы можно исключить уравнение, которое не участвует в образовании базисного минора. Таким образом, канонические уравнения прямой в пространстве будут эквивалентны системе из двух линейных уравнений с тремя неизвестными, которые и являются уравнениями пересекающихся плоскостей, причем линией пересечения этих плоскостей будет прямая, определяемая каноническими уравнениями прямой вида .

Для ясности приведем подробное решение примера, на практике все проще.

Пример.

Напишите уравнения двух пересекающихся плоскостей, которые определяют прямую, заданную в прямоугольной системе координат Oxyz в пространстве каноническими уравнениями прямой. Напишите уравнения двух пересекающихся по этой прямой плоскостей.

Решение.

Приравняем попарно дроби, образующие канонические уравнения прямой:

Определитель основной матрицы полученной системы линейных уравнений равен нулю (при необходимости обращайтесь к статье ), а минор второго порядка отличен от нуля, примем его в качестве базисного минора. Таким образом, ранг основной матрицы системы уравнений равен двум, причем третье уравнение системы не участвует в образовании базисного минора, то есть, третье уравнение можно исключить из системы. Следовательно, . Так мы получили требуемые уравнения двух пересекающихся плоскостей, определяющих исходную прямую линию.

Ответ:

Список литературы.

• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.